° Old relativistic
proverb meaning there's no place like home
(as the clockie ticks at home, it ticks nowhere)
|
|
Discover and manipulate SRT features interactively
|
|
SRT in Desmos
|
|
The following examples are Desmos files, allowing toying
with the parameters and animating the example. The first
three examples are my axiomatic approach of SRT:
understanding them will result in understanding the core
of SRT features, including why light speed has to be
constant: it is the common property of the functioning of
all light clocks!
|
The "Working with light clocks" and "Measuring and seeing
relativistic motion" sections are set in space diagrams:
x,y or even x,y,z coordinate systems (z in perspective).
The "Minkowski graphs" section is, as its name
tells, set in space-time diagrams: x,ct coordinates
(c=light speed; light signals are x=+/-ct, ie 45° lines
and their parallels).
|
Working
with light clocks
|
|
Light clocks and why there is time dilation
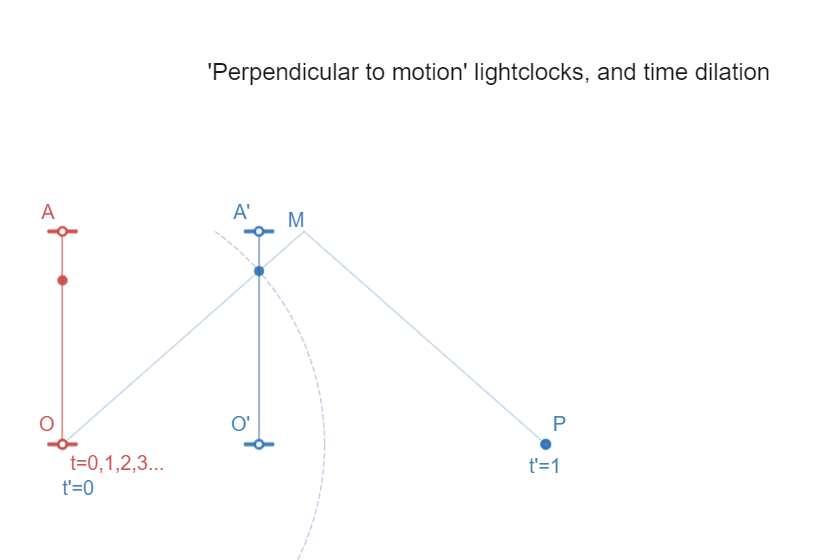
|
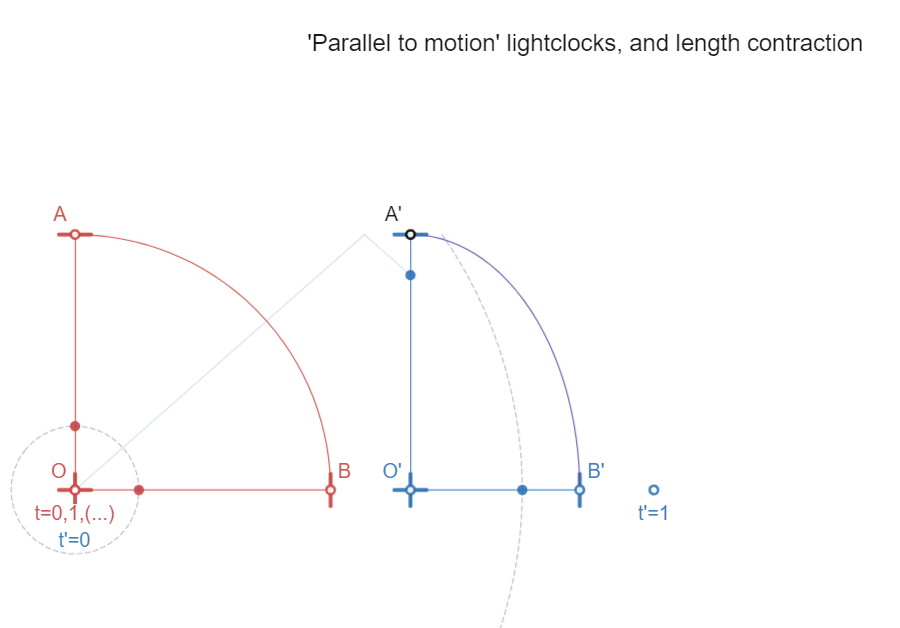
Light clocks and why there is length contraction
|
Light clocks and why there is relative
simultaneity
|
Light clocks and why there is constant light
speed
Identical light clocks are defined as
- in own (rest) inertial system: ticking in pace
(defining equality of length)
- in other (moving) inertial systems: same length
perpendicular to direction of motion
(implying
time dilation due to longer light paths, and
length contraction for light clocks along direction
of motion, to keep "ticking in pace" with their
perpendicular equals)
All light clocks will "measure" the same light speed,
since equal clock lengths imply equal clock time, and
proportional lengths proportional time. Light speed has
got to be a common constant in this light clock model.
|
Light clocks and why there is relativistic
mass
I'm not developing this theme here, but for the
following shortcut.
Defining light clocks on given wave lengths of the light
photons involved, we can define the combined impulse p
"carried" by the photons in one clock cycle, and then
define the light clock's energy as E=pc, and its mass m
as mv=p where v is the light clock's velocity WRT a rest
system. All this leads to m(v)=m(0)*gamma(v). Light
clocks carry relativistic "mass" with them!
My shortcut adage is: light clocks are light speed's
trick to carry mass at infraluminal velocities.
|
Light clocks, and SRT axioms
Using these light clock features as axioms for SRT,
one gets a true intuitive feel of it.
Instead of learning that
A counterintuitive constant light speed tells space and
time how to express matter (and clocks, meters, and
light clocks)
I prefer learning that
Light clocks and their light play tell matter how to
express space and time
(in its own substance, its meters and clocks, and in
constant light speed)!
|
Lorentz
transform properties
|
|
Reciprocity of length contraction
An animated example with a moving object WRT an object
at rest
(See also under Minkowski graphs)
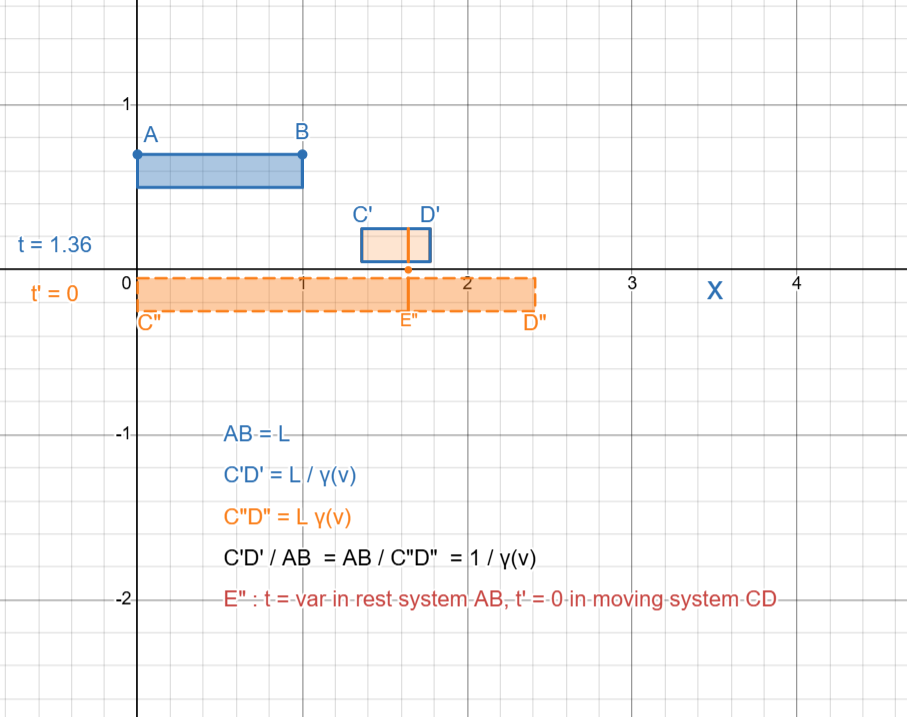
|
Reciprocity of length contraction 3D
Like the previous, in a 3D setting
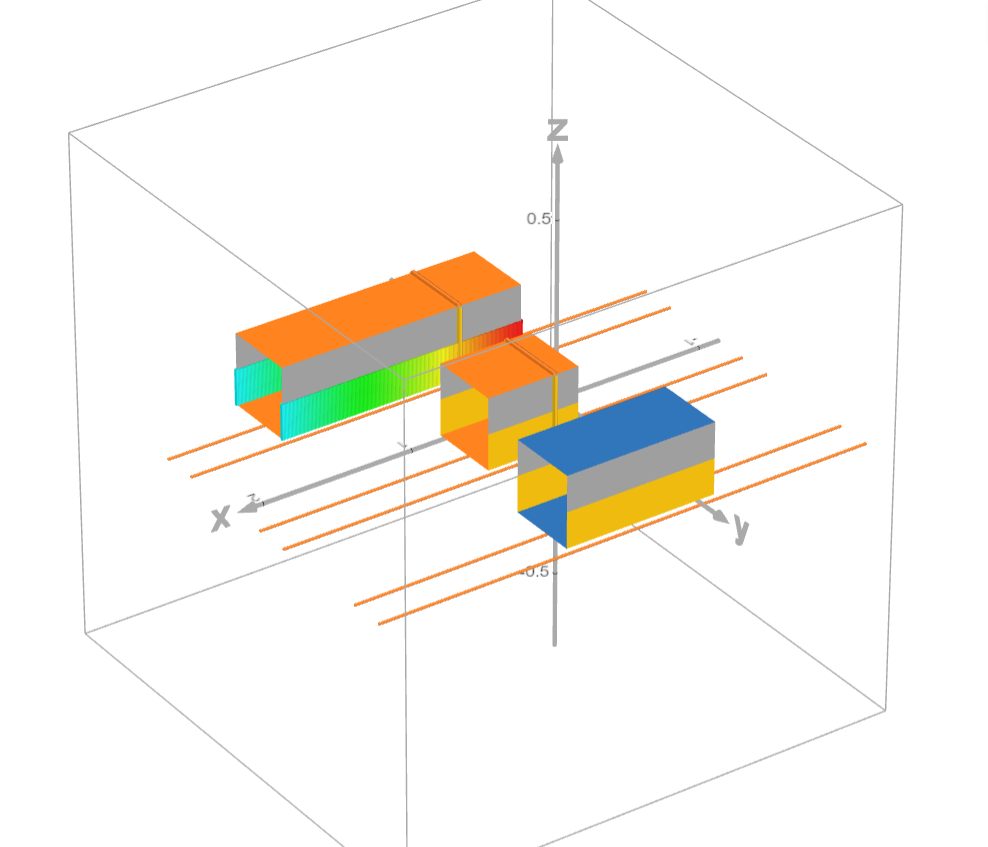
|
Measuring
relativistic
motion, and Seeing it
|
|
The above (Lorentz transform) features are
reciprocal properties in moving inertial systems. They are
results of measuring and (back-)calculating
coordinates.
Actually looking at relativistic
motion involves an additional process: Doppler effects,
due to light reaching the observer's eye or camera,
arriving with different delays from different parts of the
moving object at a single moment.
|
In the following examples, everytime both the "Lorentz"
(features measured) and "Doppler" object (object as
seen, I also call them "Einstein" object) are
shown.
|
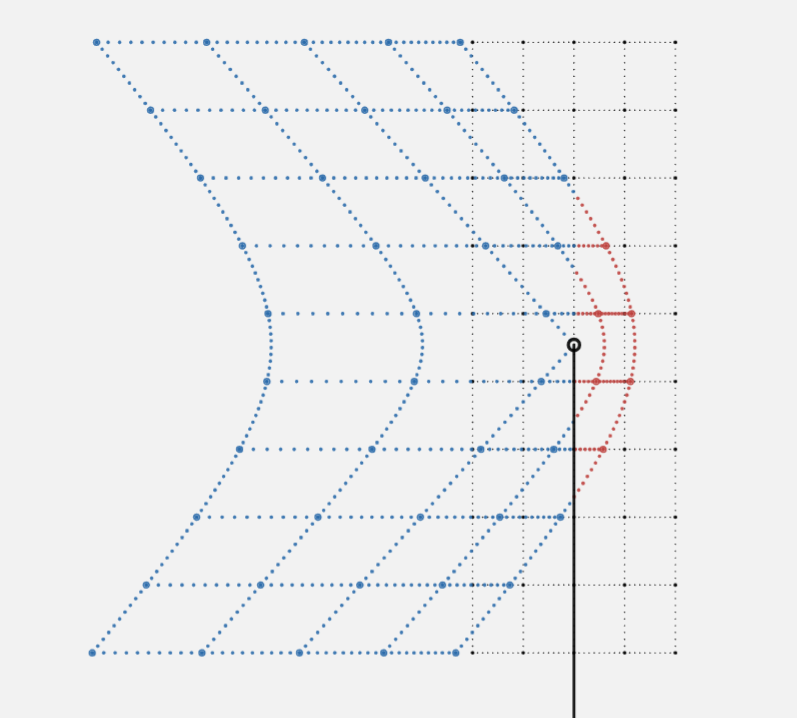
Looking at... a Square
|
... a Circle
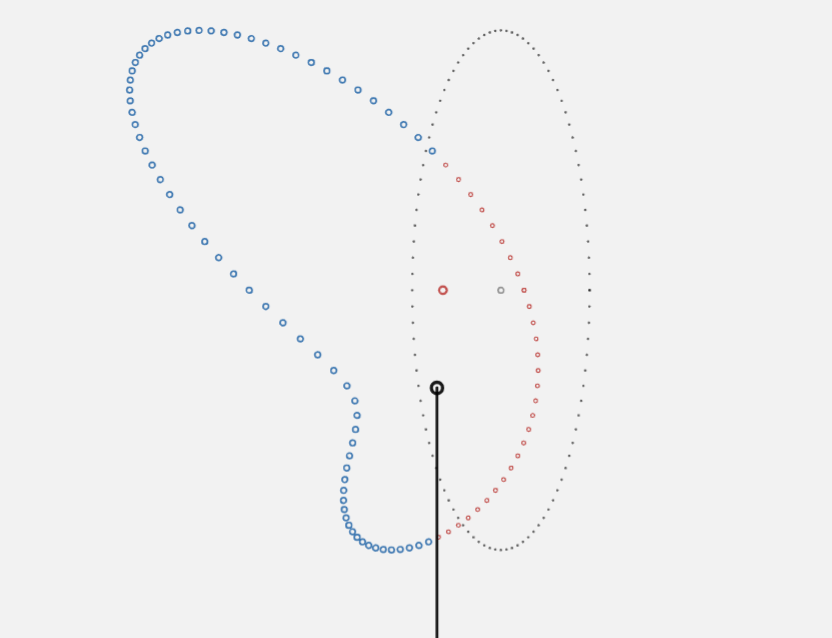
|
a joined circle and square
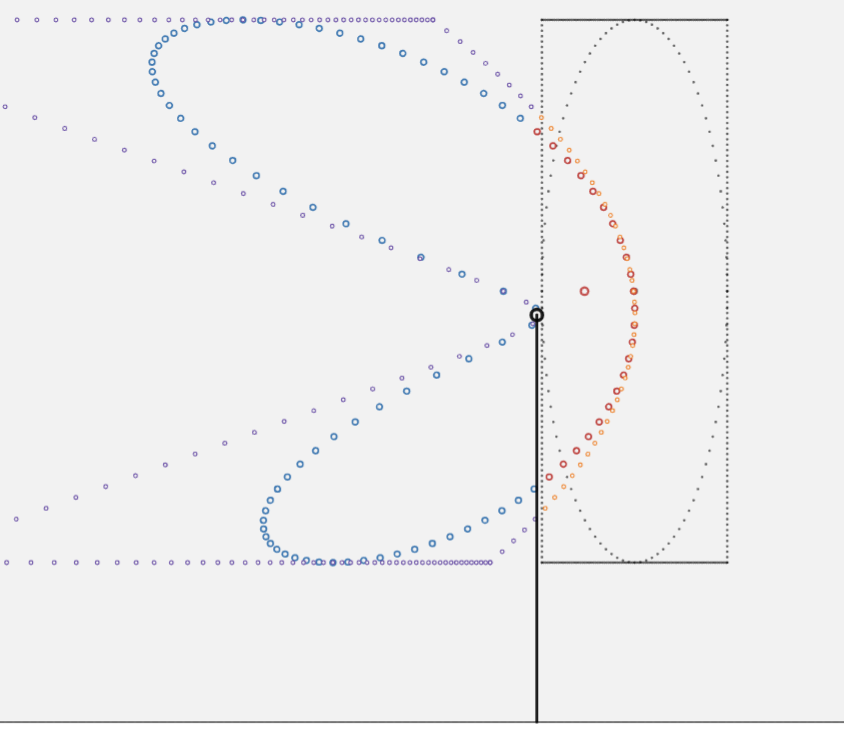
|
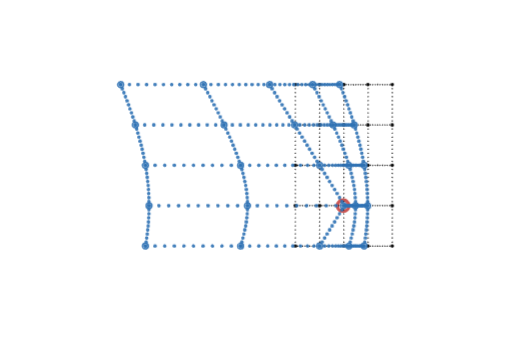
a grid, or "squadron of squares"
|
a long, long train passing by an observer on
the platform
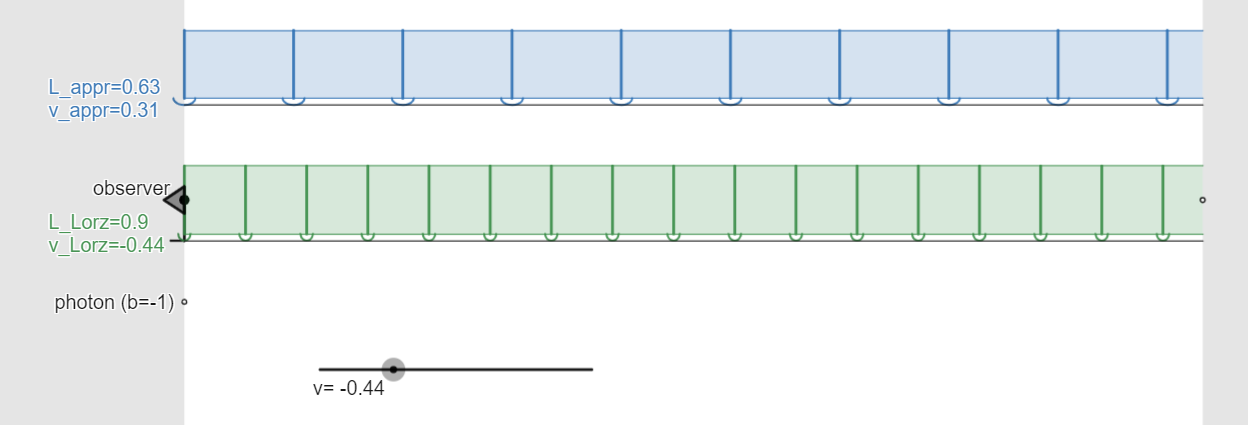
|
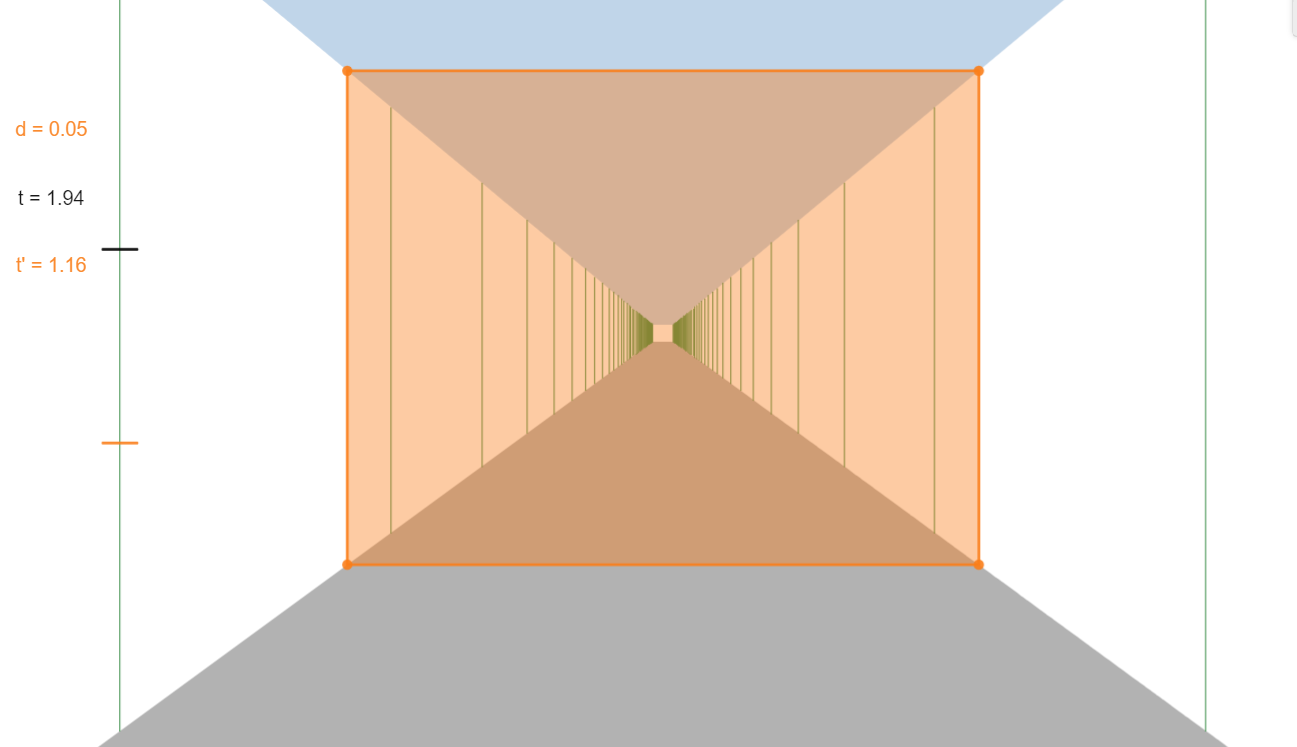
a train seen in perspective from the platform
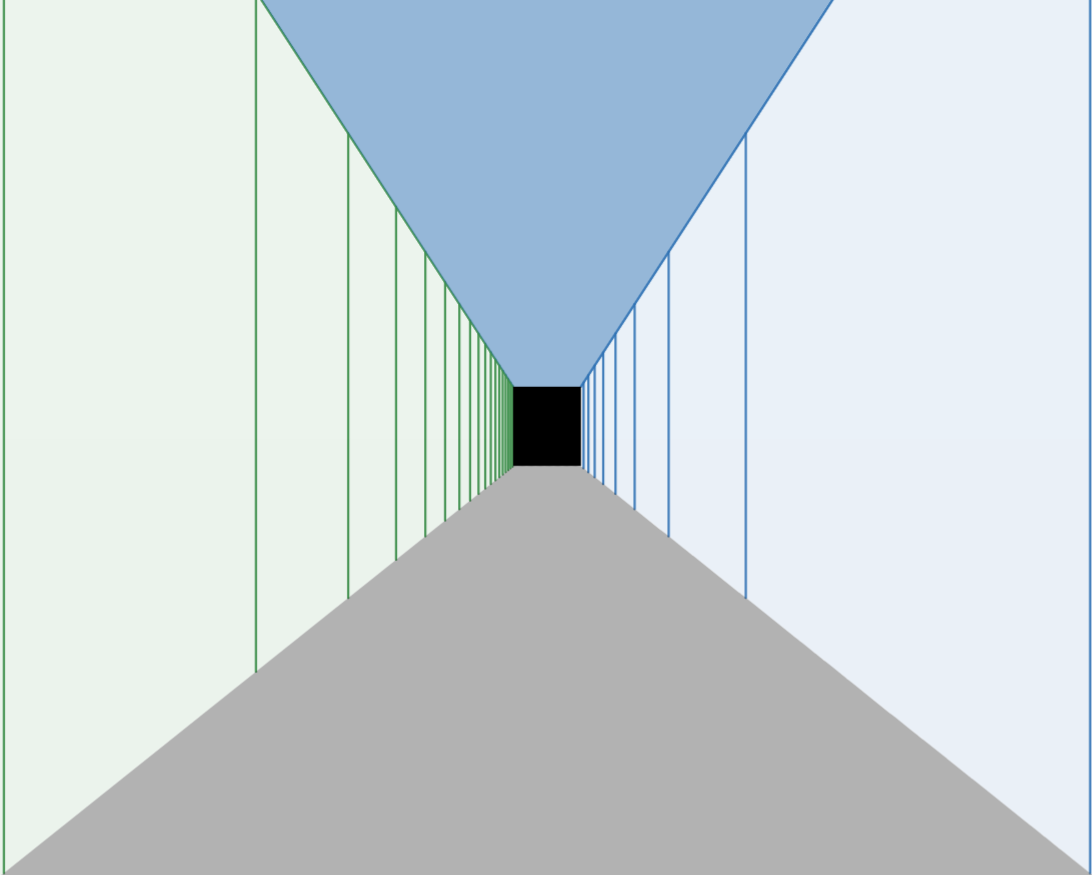
|
a Twin Paradox (TP) simulator
(Lorentz and Doppler cases, each with POV of homestayer
and traveler)
|
|
Minkowski
graphs
|
|
These graphs are coordinate systems for spacetime, itself
a model for our universe's (local) structure. The
one-dimensional case displays the (x,ct) coordinates of an
inertial system "at rest" and (x',ct') of systems moving
along.
|
The choice of x and ct coordinates results in light speed
signals having 45° line equations x=ąct and x'=ąct',
or parallels to those. The perpendicularity of x and ct
axes is arbitrary and has no physical meaning.
|
Reciprocity of Lorentz transforms:
length contraction and time dilation
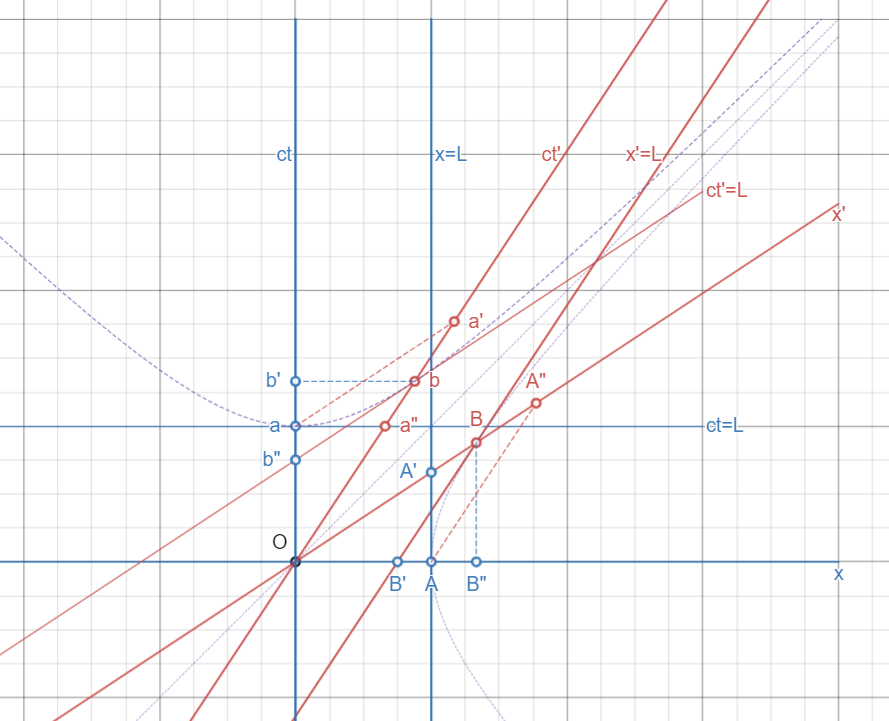
|
Reciprocity of length contraction
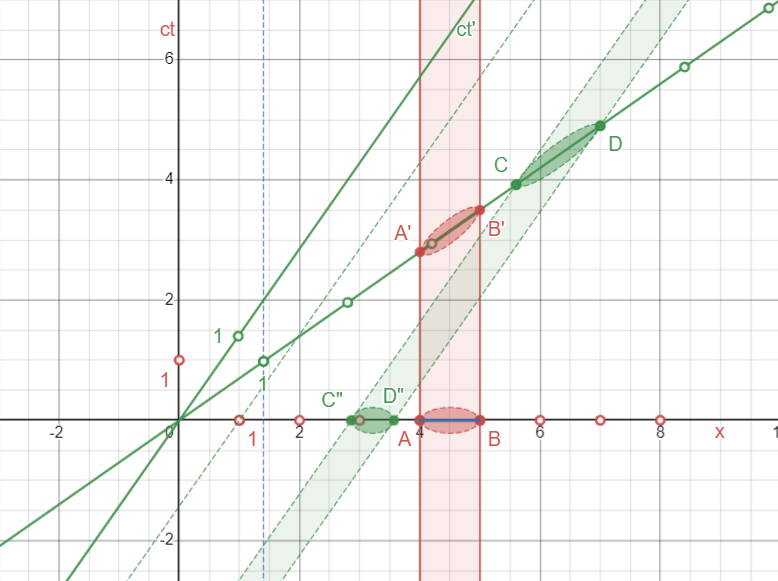
|
Reciprocities of Minkowski:
(1) state of motion: "rest" vs. "moving", and
(2) Lorentz transforms: length contraction and time
dilation
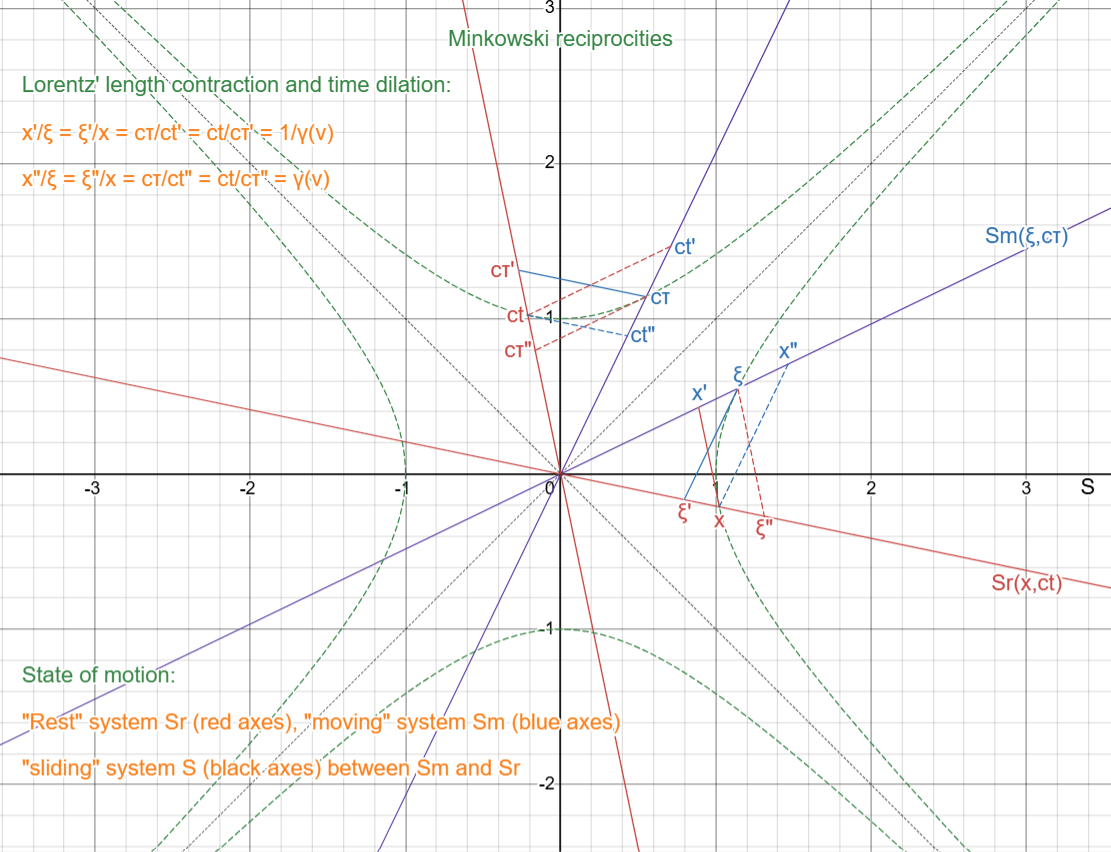
|
|
Twin Paradox with length contraction and Born-rigid
acceleration:
POV of traveller
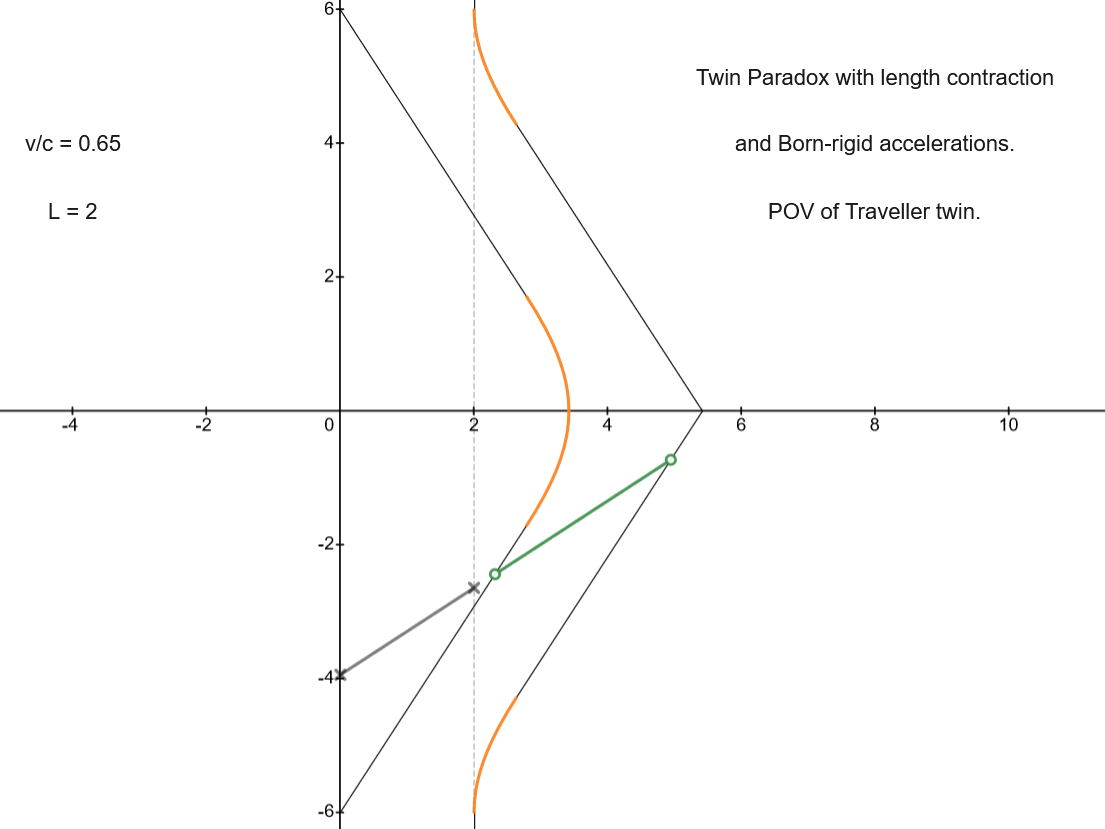
|
Twin Paradox with length contraction (and Born-rigid
acceleration):
POV of homestayer
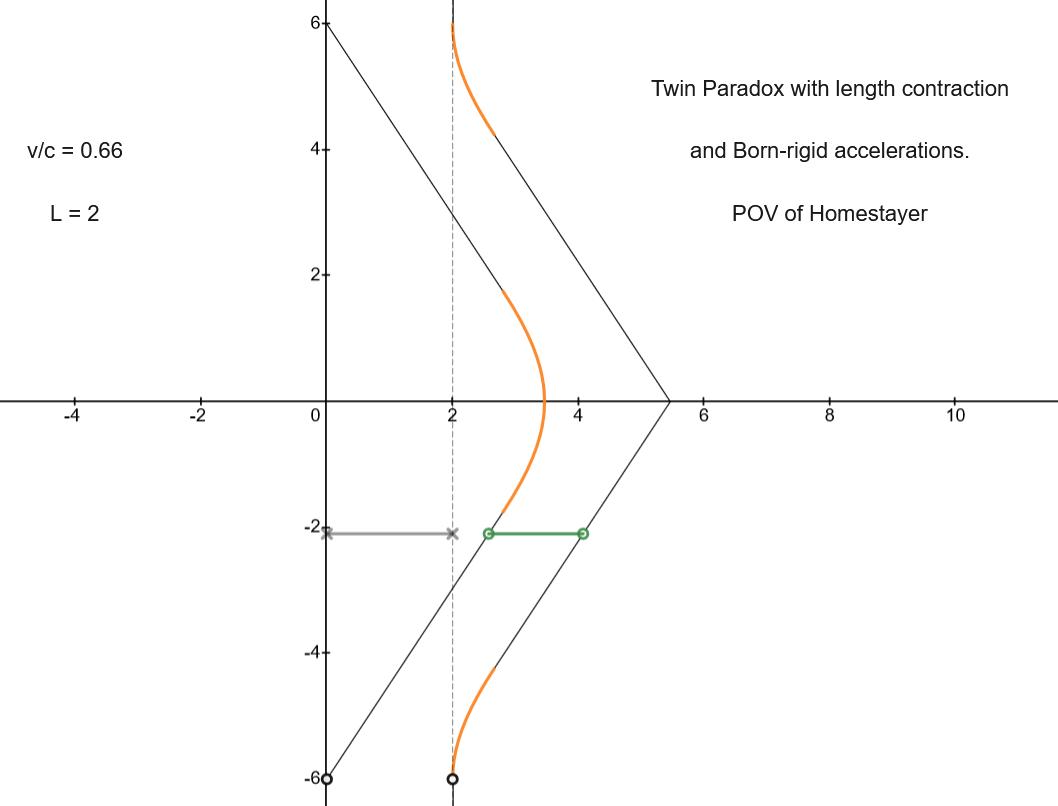
|
Bell's spaceship paradox
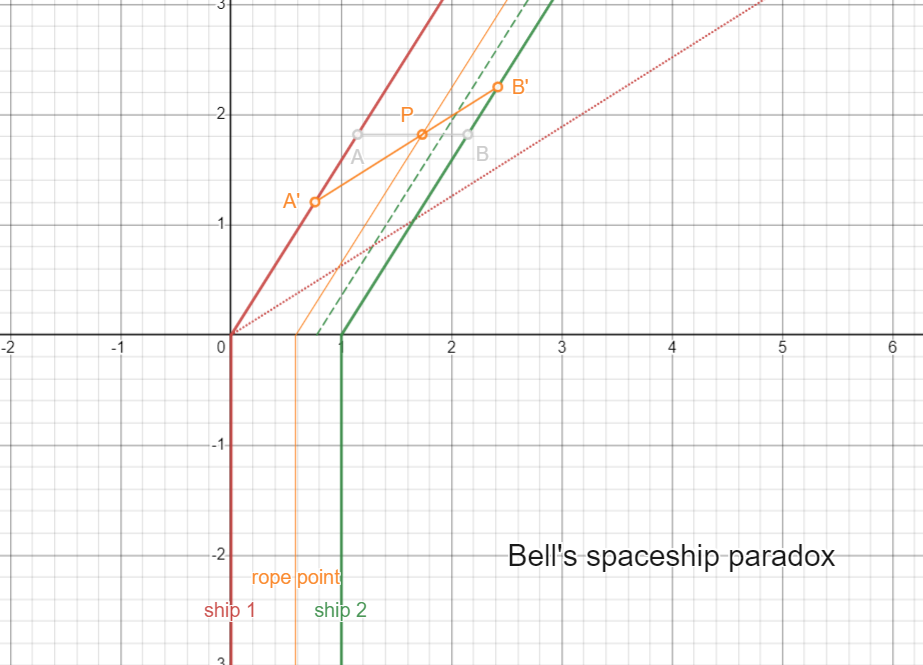
(Any point P of the rope finds the rope under
non-contracted stress once in motion.)
|
|
|
|

